Orthogonal Arrays
The Orthogonal Array Testing method is a technique used to reduce the number of test scenarios required to cover all possible combinations of inputs.
It utilizes specially designed mathematical structures known as orthogonal arrays, which enable the testing of individual factors independently while minimizing the number of test scenarios.
These arrays are designed to minimize test redundancy and ensure that each variable and its combinations are tested in various combinations with other variables. Each variable has its own range of values, and each value is tested in different combinations with values of other variables. More
It utilizes specially designed mathematical structures known as orthogonal arrays, which enable the testing of individual factors independently while minimizing the number of test scenarios.
These arrays are designed to minimize test redundancy and ensure that each variable and its combinations are tested in various combinations with other variables. Each variable has its own range of values, and each value is tested in different combinations with values of other variables. More
Covering Arrays
This technique, much like Orthogonal arrays, is key to ensuring sufficient coverage of various input value combinations without burdening extensive and time-consuming testing of all possible combinations.
These tests are designed to minimize testing redundancy while ensuring that each combination of input values is covered by at least one test scenario.
Unlike Orthogonal arrays, which always work with pairs of combinations, with Covering arrays, you can choose the so-called strength of the array, determining whether test scenarios will be combinations of pairs, triples, or other n-tuples.
Of course, the larger the n-tuple chosen for combinations, the greater the coverage will be, but the resulting number of test scenarios will also be higher. However, it's advisable to use variables for Covering arrays that have the same number of values. Less More
These tests are designed to minimize testing redundancy while ensuring that each combination of input values is covered by at least one test scenario.
Unlike Orthogonal arrays, which always work with pairs of combinations, with Covering arrays, you can choose the so-called strength of the array, determining whether test scenarios will be combinations of pairs, triples, or other n-tuples.
Of course, the larger the n-tuple chosen for combinations, the greater the coverage will be, but the resulting number of test scenarios will also be higher. However, it's advisable to use variables for Covering arrays that have the same number of values. Less More
Arrays Tool.xlsm (331kB)
Download
What are the differences between them?
- In the orthogonal array technique, each variable can have a different number of values; however, the resulting combinations are always the result of combinations of pairs of values of different variables.
- Covering arrays are suitable for variables that have the same or very similar number of values. At the same time, it is advisable to use Covering arrays when you need higher coverage or want more combinations, which the strength of the array used in Covering arrays allows you to achieve.
How to work with the Arrays Tool?
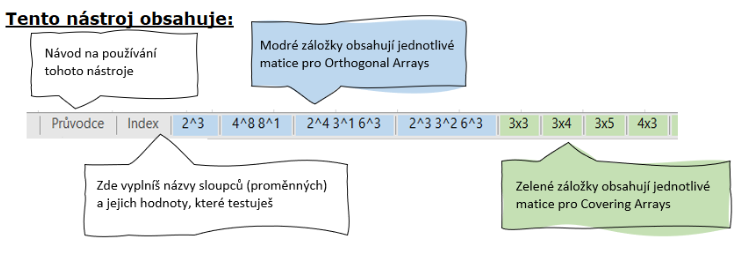
In the Arrays tool, on the Guide tab, you will find detailed instructions on how to work with the tool.
All you need to do is decide which of the above methods you want to use.
For Covering arrays, it's straightforward. On the Index tab, choose a matrix (input table) that has as many columns as you have variables and as many rows as each variable has values.
Tip: If you want to use Covering arrays and the variables do not have the same number of values, fill in empty cells in the column with one or more values that are already in that column - repeat some of the entered values of the variable so that the entire table is filled out.
Clicking on "display" will show you the generated combinations for the matrix you selected. Each output table is labeled with the strength of the array (Strength = 2 means that pairs of combinations are used in this table, Strength = 3 then triples, etc.). One row of the table equals 1 test.
For Orthogonal arrays, the procedure is as follows. Each column in the input table represents one variable, or the values that this variable can take.
The number of columns will therefore correspond to the number of variables we need to combine. The number of rows then corresponds to the highest number of values that any of these variables can take. After filling in the values and clicking on "display", the resulting matrix of combinations will be displayed on the list.
In the output table, you will find the resulting set of test scenarios, where one row equals 1 test. If any of the columns contain only null values, it is not an error but a specific form of the orthogonal matrix used. Ignore such columns.
Tip: We recommend carefully reviewing this set before using it, removing combinations that can never occur, and supplementing the set with additional business-relevant combinations.
Example for using Orthogonal arrays:
I have a form that contains 4 fields (variables). 3 of them (Politically exposed person / Registered at the Labor Office / Currently in execution or insolvency) can only take 2 values (Yes/No). The last variable (Marital status) can take 4 values (Single / Married / Widow, Widower / Divorced)
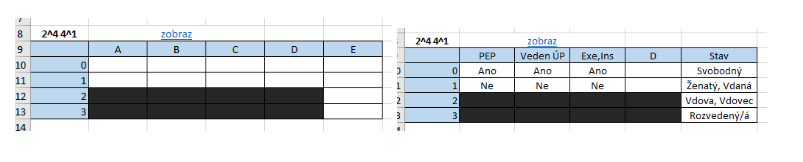
In the Arrays tool, I review the list of matrices on the Index tab and select a suitable one. Unfortunately, none of them exactly matches the parameters I have, so I have to choose the closest suitable one. For example, this one (unfilled -> filled):
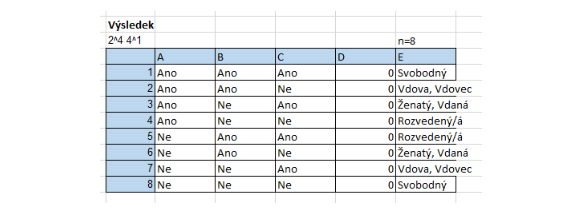
You will see a table with the resulting combinations:
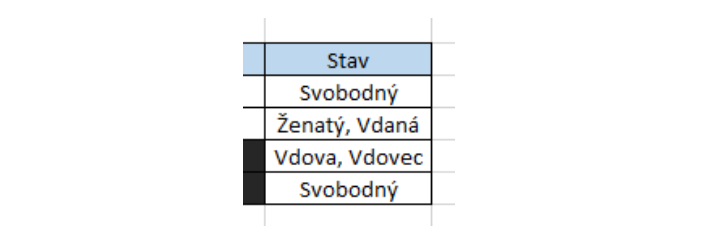
Tip: If you select a matrix where you have an extra column (you have fewer variables than there are columns in the matrix), simply skip this column (see example). If you have a variable that has fewer values than there are rows in the matrix for that variable (for example, for the Status variable, there would be only 3 options - Single, Married, Divorced), then you need to repeat one value in the last field, like this:
More

In the Arrays tool, on the Guide tab, you will find detailed instructions on how to work with the tool.
All you need to do is decide which of the above methods you want to use.
For Covering arrays, it's straightforward. On the Index tab, choose a matrix (input table) that has as many columns as you have variables and as many rows as each variable has values.
Tip: If you want to use Covering arrays and the variables do not have the same number of values, fill in empty cells in the column with one or more values that are already in that column - repeat some of the entered values of the variable so that the entire table is filled out.
Clicking on "display" will show you the generated combinations for the matrix you selected. Each output table is labeled with the strength of the array (Strength = 2 means that pairs of combinations are used in this table, Strength = 3 then triples, etc.). One row of the table equals 1 test.
For Orthogonal arrays, the procedure is as follows. Each column in the input table represents one variable, or the values that this variable can take.
The number of columns will therefore correspond to the number of variables we need to combine. The number of rows then corresponds to the highest number of values that any of these variables can take. After filling in the values and clicking on "display", the resulting matrix of combinations will be displayed on the list.
In the output table, you will find the resulting set of test scenarios, where one row equals 1 test. If any of the columns contain only null values, it is not an error but a specific form of the orthogonal matrix used. Ignore such columns.
Tip: We recommend carefully reviewing this set before using it, removing combinations that can never occur, and supplementing the set with additional business-relevant combinations.
Example for using Orthogonal arrays:
I have a form that contains 4 fields (variables). 3 of them (Politically exposed person / Registered at the Labor Office / Currently in execution or insolvency) can only take 2 values (Yes/No). The last variable (Marital status) can take 4 values (Single / Married / Widow, Widower / Divorced)
In the Arrays tool, I review the list of matrices on the Index tab and select a suitable one. Unfortunately, none of them exactly matches the parameters I have, so I have to choose the closest suitable one. For example, this one (unfilled -> filled):

You will see a table with the resulting combinations:

Tip: If you select a matrix where you have an extra column (you have fewer variables than there are columns in the matrix), simply skip this column (see example). If you have a variable that has fewer values than there are rows in the matrix for that variable (for example, for the Status variable, there would be only 3 options - Single, Married, Divorced), then you need to repeat one value in the last field, like this:

More
